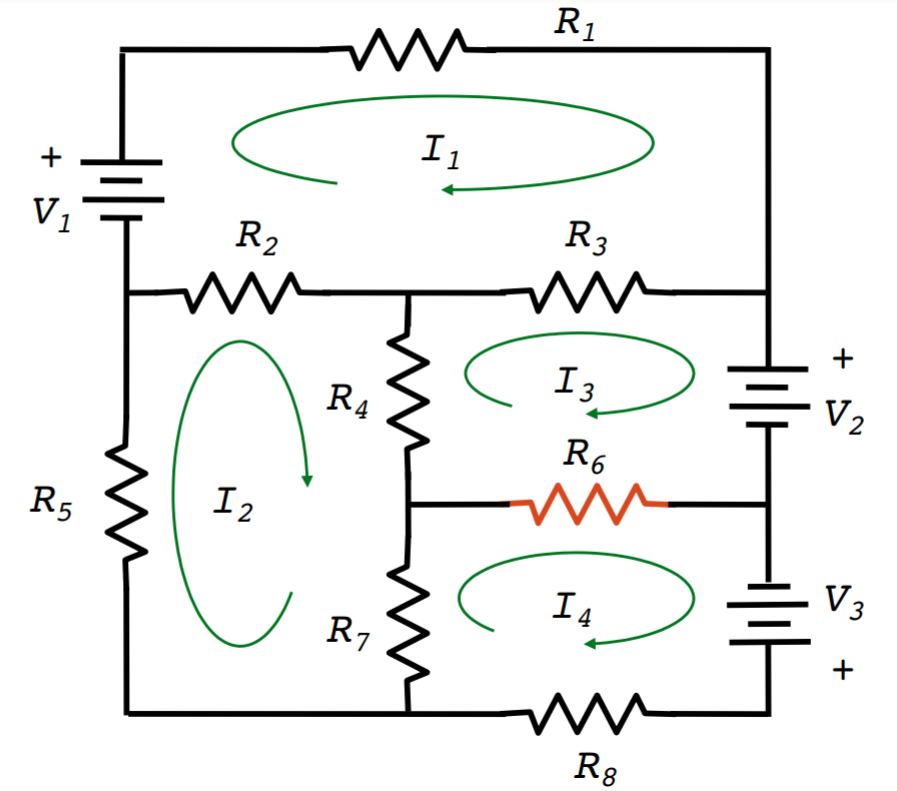
Activity 4.12.
(a)
First, solve for the current through \(R_6\) in the lumped circuit. What is the current through \(R_6\text{?}\)Answer.
\(I_3 - I_4\)
(b)
To find all unknown currents, use Kirchoff’s Voltage Law:
\begin{equation*}
\Sigma_{loop} \ V_i = 0
\end{equation*}
What are the equations for each current loop?
Answer.
\begin{equation*}
V_1 - I_1R_1 + (I_3-I_1)R_3 + (I_2-I_1)R_2 = 0
\end{equation*}
\begin{equation*}
-I_2R_5 + (I_1-I_2)R_2 + (I_3-I_2)R_4 + (I_4-I_2)R_7 = 0
\end{equation*}
\begin{equation*}
-V_2 + (I_4-I_3)R_6 + (I_2-I_3)R_4 + (I_1-I_3)R_3 = 0
\end{equation*}
\begin{equation*}
V_3 - I_4R_8 + (I_2-I_4)R_7 + (I_3-I_4)R_6 = 0
\end{equation*}
(c)
Rewrite the equations in matrix form:
\begin{equation*}
R \ I = V
\end{equation*}
Recall that we used to call the coefficient matrix A (not R) and the vector of unknowns x (not I). We used to call the right-hand side b (not V).
\begin{equation*}
A \ x = b
\end{equation*}
Answer.
\begin{equation*}
\begin{bmatrix}
-(R_1+R_2+R_3) & R_2 & R_3 & 0 \\
R_2 & -(R_2+R_4+R_5+R_7) & R_4 & R_7 \\
R_3 & R_4 & -(R_3+R_4+R_6) & R_6 \\
0 & R_7 & R_6 &-(R_6+R_7+R_8)
\end{bmatrix}
\begin{bmatrix}I_1\\I_2\\I_3\\I_4\end{bmatrix} =
\begin{bmatrix}-V_1\\0\\V_2\\-V_3\end{bmatrix}
\end{equation*}
(d)
Put some numbers in for the known quantities:
\begin{equation*}
V_1 = 20V \ \ \ \ \ R_1 = 18\Omega \ \ \ \ \ R_4 = 6\Omega \ \ \ \ \ R_7 = 12\Omega
\end{equation*}
\begin{equation*}
V_2 = 12V \ \ \ \ \ R_2 = 10\Omega \ \ \ \ \ R_5 = 15\Omega \ \ \ \ \ R_8 = 12\Omega
\end{equation*}
\begin{equation*}
V_3 = 40V \ \ \ \ \ R_3 = 16\Omega \ \ \ \ \ R_6 = 8\Omega
\end{equation*}
(e)
Try solving this in MATLAB.
Answer.
>> V1 = 20; V2 = 12; V3 = 40; % create voltages (V) >> R1 = 18; R2 = 10; R3 = 16; % create resistances >> R4 = 6; R5 = 15; R6 = 8; % (Ohms) >> R7 = 12; R8 = 14;
% create resistance matrix R
>> R = [-(R1+R2+R3)
R2 R3 R2 -(R2+R4+R5+R7)
R4 R7 R3 R4 -(R3+R4+R6)
R6 0 R7 R6 -(R6+R7+R8)];
>> V = [-V1; 0; V2; -V3];
>> I = R\V
I =
0.8411
0.7206
0.6127
1.5750
>> I(3)-I(4)
ans =
-0.9623