Section 4.8 Element-by-Element Operators
It is also possible to do element-by-element calculations with arrays. For example, if you have two row vectors you may wish to compute the product of the elements of each vector, just element by element as described here:
\(x = \begin{bmatrix} x_1 & x_2 & x_3 & x_4 \end{bmatrix}\) and \(y = \begin{bmatrix} y_1 & y_2 & y_3 & y_4 \end{bmatrix}\)
\(\begin{bmatrix}(x_1 \times y_1) & (x_2 \times y_2) & (x_3 \times y_3) & (x_4 \times y_4)\end{bmatrix}\)
Since both x and y are \(1\times 4\) matrices we cannot multiply them using the linear algebra matrix multiplication (inner dimensions don’t agree). We’d have to transpose one of the two vectors and then go from there.
Similarly, we may be interested in quotients instead or in exponentiation as shown here:
\(\begin{bmatrix}(x_1 \div y_1) & (x_2 \div y_2) & (x_3 \div y_3) & (x_4 \div y_4)\end{bmatrix}\)
\(\begin{bmatrix}x_1^n & x_2^n & x_3^n & x_4^n\end{bmatrix}\)
\(\begin{bmatrix}x_1^{y1} & x_2^{y2} & x_3^{y3} & x_4^{y4}\end{bmatrix}\)
All of the these are called element-by-element operations and MATLAB can perform these easily (without having to write a loop as you would have to do in C!)
You might even consider matrices of the same size for which you’d like to perform operations element-by element:
\(A = \begin{bmatrix}
a_{11} & a_{12} & a_{13}\\
a_{21} & a_{22} & a_{23}\\
a_{31} & a_{32} & a_{33}\\
\end{bmatrix},
B = \begin{bmatrix}
b_{11} & b_{12} & b_{13}\\
b_{21} & b_{22} & b_{23}\\
b_{31} & b_{32} & b_{33}\\
\end{bmatrix}\)
You might wish to find
\(\begin{bmatrix}
a_{11}\times b_{11} & a_{12}\times b_{12} & a_{13}\times b_{13}\\
a_{21}\times b_{21} & a_{22}\times b_{22} & a_{23}\times b_{23}\\
a_{31}\times b_{31} & a_{32}\times b_{32} & a_{33}\times b_{33}\\
\end{bmatrix}\)
or
\(\begin{bmatrix}
a_{11}\div b_{11} & a_{12}\div b_{12} & a_{13}\div b_{13}\\
a_{21}\div b_{21} & a_{22}\div b_{22} & a_{23}\div b_{23}\\
a_{31}\div b_{31} & a_{32}\div b_{32} & a_{33}\div b_{33}\\
\end{bmatrix}\)
Let’s now take a look at how to perform these element-by-element operations in MATLAB:
Subsection 4.8.1 Element-by-Element Operators
For calculations which involve each element of an array or matrix, we use the element-by-element operators (or dot operators):
-
multiplication:
.* -
exponentiation:
.^ -
right division:
./ -
left division:
.\
Here are some examples:
>> A = [2 6 3; 5 8 4]; % 2x3 arrays >> B = [1 4 10; 3 2 7]; >> A.*B
ans =
2 24 30 %2x3 element-by-element result
15 16 28
What’s wrong with multiplying the following two matrices A and B together?
>> A = [2 6 3; 5 8 4]; % 2x3 arrays >> B = [1 4 10; 3 2 7]; >> A*B % 2x3 2x3
\(\color{red}{\text{??? Error using ==> * Inner matrix dimensions must agree.}}\)
Since we are working element-by-element, clearly the two matrices must have the same dimensions.
How can we square each element of a matrix using the element-by-element operators?
>> A = [2 6 3; 5 8 4]; % 2x3 arrays >> B = [1 4 10; 3 2 7]; >> A.^2 % square each element
ans =
4 36 9
25 64 16
Now, let’s try raising each element of the matrix A to the power of elements in matrix B:
>> A.^B
ans =
2 296 59049
125 64 16384
Subsection 4.8.2 Dot Operator Example
One often uses the dot operators to compute the values of a function at many values of its argument(s). For example, suppose we wanted to graph the fifth order polynomial:
\begin{equation*}
y = x^5 - 5x^4 + 10x - 5
\end{equation*}
In order to do so we’ll need to find the y-values for lots and lots of different x-values. In C, this would mean writing a loop over all of those x-values. In MATLAB, we can make use of element-by-element operations:
>> x = 0:0.1:100; % 1001 points from 0 to 100 >> y = x.^5 - 5*x.^4 + 10*x - 5; >> plot(x,y)
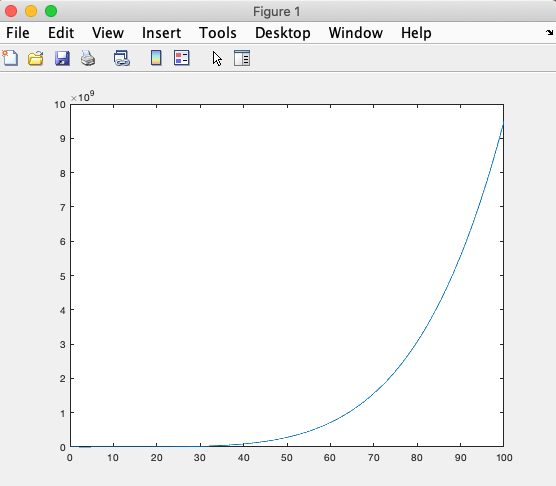
We must use dot operators here! Take a look at what happens if we don’t...:
>> y = x^5 - 5*x^4 + 10*x - 5;
\(\color{red}{\text{??? Error using ==> mpower ... Matrix must be square.}}\)

