Section 5.2 Storing Positive Integers

Computers speak in binary, which is how integers are stored in memory.

Let’s start by reviewing binary numbers:

Aside: Video Description.

Figure 5.1.

Investigate 5.3.

What is the decimal value of 01000001?

Computers "speak" in binary (base-2) only, which includes only 1s and 0s.

Bit: one binary digit (0 or 1)
Byte: number of bits used to represent a character, almost always 8 bits
Word: natural unit of memory for a given computer design; unit of data that can pass across the bus to or from main memory at one time

For example, in the 8-digit binary number 01100110, the left-most bit is the Most Significant Bit, and the right-most bit is the Least Significant Bit.

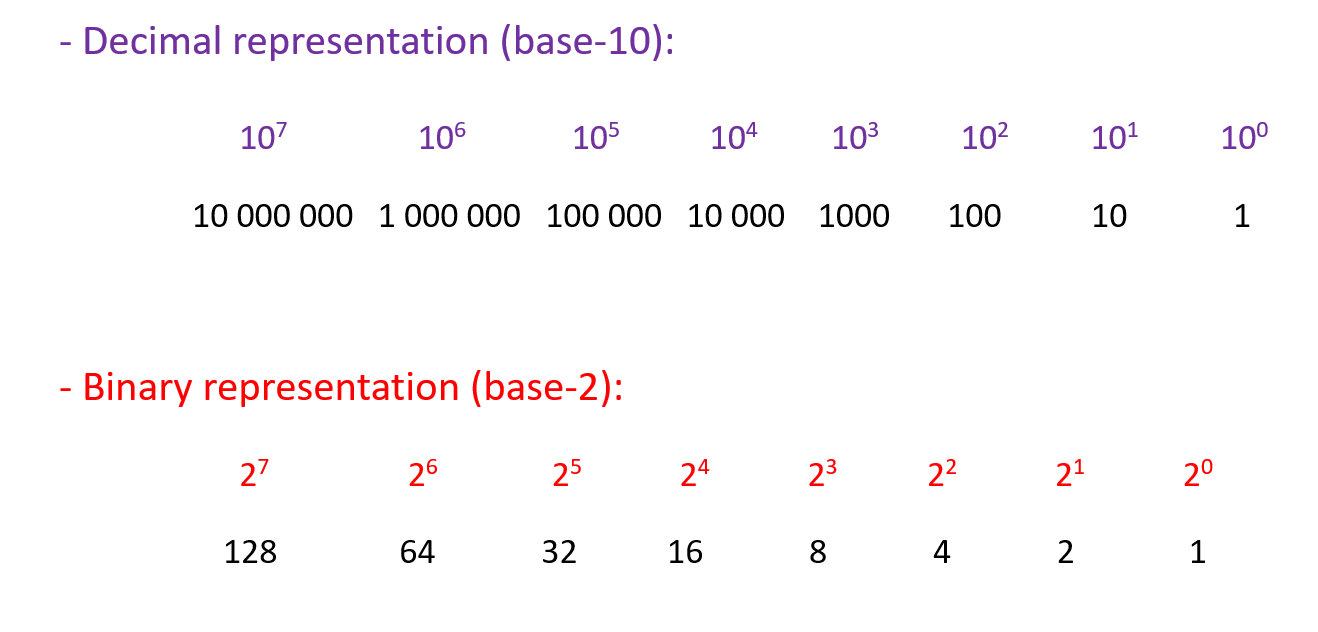
In decimal (base-10), the number 135 can be represented as:

\begin{equation*} 135 = 1\cdot 10^2 \; + \; 3\cdot 10^1 \; + \; 5\cdot 10^0 \end{equation*}

where \(10^2\) is the "hundreds" place, \(10^1\) is the "tens" place, and \(10^0\) is the "ones" place.

Instead of base-10, what if we have base-b?

\begin{equation*} (number)_b = a_nb^n + a_{n-1}b^{n-1} + ... + a_0b^0 \end{equation*}

\(b\text{:}\) base (binary: 2, decimal: 10, ...)
\(a_k\text{:}\) digits (binary: 0-1, decimal: 0-9, in general 0-(b-1))
\(n\text{:}\) position of "most significant digit" (MSD)

Special case: base \(b = 2\) (binary) -- note: in binary there are only two different digits: 0 and 1

Note: Digits have different weights (place values)

Check Your Understanding Check Your Understanding

1.

Find the decimal value of each of the following binary numbers:

00110001
11111110
10011001

2.

How many bits are there in one byte?

Next, we’ll learn how to convert between different binary and decimal representations:

Aside: Video Description.

Investigate 5.4.

What is the remainder when dividing 50 by 3?

How do we convert from one base to another?

In particular, how do we find the binary representation (base-2) of a decimal number (base-10)?

Example: What is 135 decimal in binary or base-2?

Hint: The easiest way to do this is to divide the number by 2 repeatedly and keep track of the remainder.

135    /2       = 67 R1     * 2^0
 67    /2       = 33 R1     * 2^1
 33    /2       = 16 R1     * 2^2
 16    /2       =  8 R0     * 2^3
  8    /2       =  4 R0     * 2^4
  4    /2       =  2 R0     * 2^5
  2    /2       =  1 R0     * 2^6
  1    /2       =  0 R1     * 2^7

 135              -> 1000 0111

Does it work? 128 + 4 + 2 + 1 = 135

and... does this work for any base?

Example: what does the algorithm say 135 is in... base-10?

135    /10      = 13 R5     * 10^0    LSD
 13    /10      =  1 R3     * 10^1
  1    /10      =  0 R1     * 10^2    MSD

 135              -> 135

Not very surprising...

There are other ways to find the binary representation of a number.

Recall the binary place values:

So...

135 = 1 * 128 + 7
  7 = 0 * 64 + 0 * 32 + 0 * 16 + 0 * 8 + 1 * 4 + 3
  3 = 1 * 2 + 1
  1 = 1 * 1
135 = 1 * 128 + 0 * 64 + 0 * 32 + 0 * 16 + 0 * 8 + 1 * 4 + 1 * 2 + 1 * 1

Thus 135 is 10000111 in binary.

Check Your Understanding Check Your Understanding

1.

What is the remainder when dividing 36 by 15?

2.

Find the 8-bit binary representation of the decimal number 222:

Prev Top Next