Skip to main content
Contents Index Dark Mode Prev Up Next \(\newcommand{\N}{\mathbb N}
\newcommand{\Z}{\mathbb Z}
\newcommand{\Q}{\mathbb Q}
\newcommand{\R}{\mathbb R}
\newcommand{\lt}{<}
\newcommand{\gt}{>}
\newcommand{\amp}{&}
\definecolor{fillinmathshade}{gray}{0.9}
\newcommand{\fillinmath}[1]{\mathchoice{\colorbox{fillinmathshade}{$\displaystyle \phantom{\,#1\,}$}}{\colorbox{fillinmathshade}{$\textstyle \phantom{\,#1\,}$}}{\colorbox{fillinmathshade}{$\scriptstyle \phantom{\,#1\,}$}}{\colorbox{fillinmathshade}{$\scriptscriptstyle\phantom{\,#1\,}$}}}
\)
Section 5.3 Storing Negative Integers
Now we know how positive integers can be stored in the computer. How about negative integers? There actually are several different options. The following video describes the
signed magnitude representation of negative numbers:
Video Description.
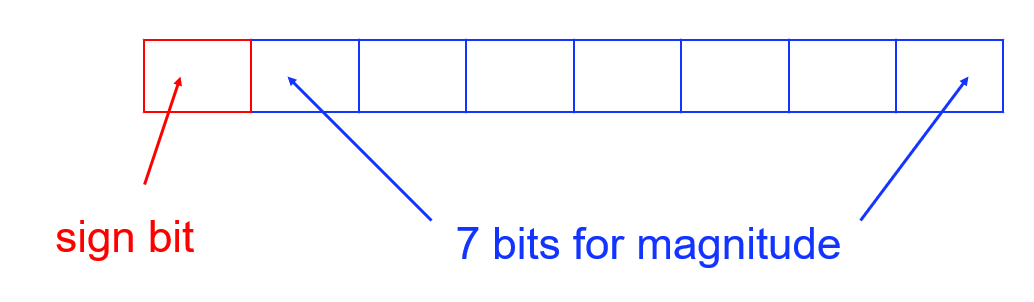
In signed magnitude representation the most significant bit is interpreted as a sign (negative or positive)
0 is negative, 1 is positive
In an 8-bit number, only 7 bits remain for the magnitude of the number
Binary adding does not work in a straight-forward manner in this representation
Investigate 5.5 .
Does the binary number
10000001 represent the
same decimal number in both unsigned binary and signed magnitude binary?
Hint .
Try converting the binary number to decimal, following the rules of each binary representation method.
We have been representing positive integers as binary numbers, what about negative integers?
Several strategies are possible:
The most obvious is known as
signed magnitude , which uses the most significant bit (MSB) for the sign:
0 for
+ and
1 for
-.
For an 8-bit binary number:
This allows for a range from -127 to 127 to be represented.
For an n-bit binary number:
\(-(2^{n-1}-1)\) to
\((2^{n-1}-1)\)
Subsection 5.3.1 Adding in Binary
How do you add binary numbers?
Recall addition in the
decimal system :
1
79 79
+ 106 + 106
______ --> ______
185 185
Notice how we "carry" the one from the ones digits (shown on the right above)? We add similarly in binary, following these rules:
1 + 0 = 01
1 + 1 = 10
Here’s an example of adding in binary (with "carrying" the ones shown on the right again):
1 111
01001111 01001111
+ 01101010 + 01101010
___________ --> ___________
10111001 10111001
We can check that this binary addition aligns with decimal addition, as 79 + 106 = 185 (as shown above).
Subsection 5.3.2 Adding in Signed Magnitude
How about adding numbers in binary when using the signed magnitude representation of integers?
Adding two positive numbers:
00001101 (13 decimal)
+ 01100100 (100 decimal)
___________
01110001 (113 decimal)
Adding a positive and a negative number:
00001101 (13 decimal)
+ 11100100 (-100 decimal)
___________
11110001 (-113 decimal)
Addition does not work with signed magnitude numbers!
Check Your Understanding 5.3.3 Check Your Understanding
1. What is the 8-bit representation of the decimal number -63, if the signed magnitude representation is used?
Subsection 5.3.4 Binary Two’s Complement
We noticed in the last video that arithmetic is not straight forward in the signed magnitude representation of negative numbers. We therefore introduce a different way to store negative integers, namely the
binary two’s complement representation. While this representation may seem cumbersome at first, the point is really to fix the problems we observed with binary addition when negative numbers are involved. The binary two’s complement representation allows for the same process to be used in adding integers internally inside the computer, regardless of whether the numbers are positive or negative. This process is typically hard-wired in the computer’s processor which makes for super fast execution time.
Video Description.
Addition works in binary 2’s compliment
To represent negative integers, find the binary of the magnitude first, then swap all 0s and 1s and finally add 1
Calculating the range of numbers that can be represented
Addition does not work with signed magnitude numbers.
Solution: use an alternative for representing signed integers known as
binary 2’s complement .
Idea: Store negative integers in such a way that when summed with its complement (positive number) the result is zero.
Rules for writing the 2’s complement of a number:
Write down the binary representation of the magnitude
Positive integers stay the same
Negative integers:
Change all 0s to 1s and all 1s to 0s
Add 1
Subsection 5.3.5 2’s Complement Example
13
+ -100
________
-87
13 --> 00001101
-100 --> 01100100
Steps 2 and 3a: binary complement
00001101 --> stays the same
01100100 --> 10011011
00001101 --> stays the same
10011011 --> 10011100
00001101
+ 10011011
___________
10101001
Did it work? Is this the 2’s complement of -87?
We need a way to decode a 2’s complement number...
Subsection 5.3.6 Decoding 2’s Complement Numbers
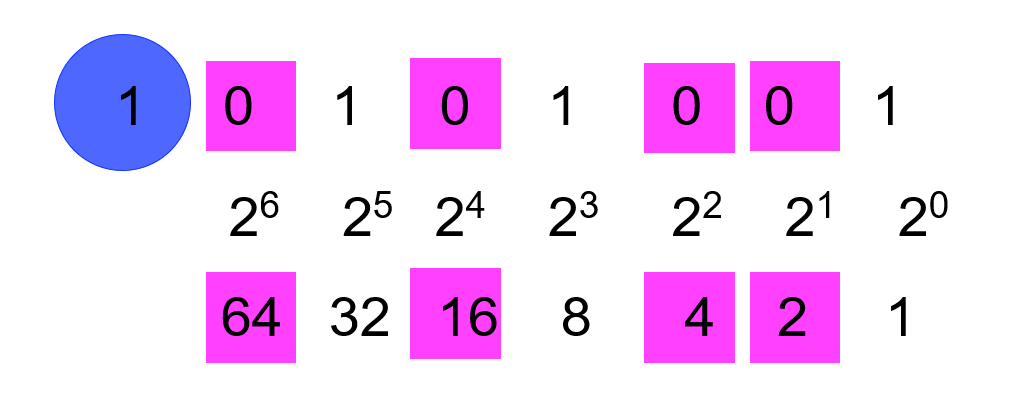
All 2’s complement numbers that are negative have MSB ’set’ (negative) -- shown in blue
Add values of the places which are zero: (64 + 16 + 4 + 2) -- shown in pink
Add one to the result
So the binary 2’s complement number 10101001 is:
-(64 + 16 + 4 + 2 + 1) = -87
So, addition with 2’s complement integers works!
Whats the range of numbers you can represent when using the binary 2’s complement?
8-bit 2’s complement numbers range: -128 to 127
n-bit 2’s complement numbers:
\(-(2^{n-1})\) to
\((2^{n-1}-1)\)
Food for thought: why is
\(2^{n-1}\) not represented in 2’s complement?
Check Your Understanding 5.3.7 Check Your Understanding
1. What is the 8-bit binary 2’s complement representation of the number 63 (careful: this is a positive number... what do positive numbers look like in 2’s complement?)
2. What is the 8-bit binary 2’s complement representation of the number -63
Subsection 5.3.8 Counting in Binary Two’s Complement
Finally, let’s take a look at what happens when counting beyond the largest possible number in binary 2’s complement.
More food for thought: start at 0, keep adding 1. What happens?
Decimal Binary Two's Complement
0 00000000
1 00000001
2 00000010
3 00000011
. .
. .
. .
126 01111110
127 01111111
+1 ?????
What is the decimal value of this 2’s complement number?
1111111 <-- carrying the ones
127 01111111
+ 1 + 00000001
______ ___________
??? 10000000
MSB is ’set’, so the number is negative
Add values of the places which are zero: 64 + 32 + 16 + 8 + 4 + 2 + 1 = 127
Add 1 to the result
Thus, the result is -128.
Check Your Understanding 5.3.9 Check Your Understanding
1. What is the decimal value of the 8-bit binary 2’s complement number
10101010?